О математических функциях

Математические функции используют при выполнении арифметических и тригонометрических вычислений, округлении чисел и в некоторых других случаях.

Суммирование

Простая сумма

Для простейшего суммирования используют функцию СУММ.

Синтаксис функции

СУММ(А),

где A – список от 1 до 30 элементов, которые требуется суммировать. Элемент может быть ячейкой, диапазоном ячеек, числом или формулой. Ссылки на пустые ячейки, текстовые или логические значения игнорируются.

Фактически данная функция заменяет непосредственное суммирование с использованием оператора сложения (+). Формула =СУММ(В2:В7), указанная в ячейке В8 (рис.1), тождественна формуле =В2+В3+В4+В5+В6+В7. Однако есть и некоторые отличия. При использовании функции СУММ добавление ячеек в диапазон суммирования автоматически изменяет запись диапазона в формуле. Например, если в таблицу вставить строку, то в формуле будет указан новый диапазон суммирования. Аналогично формула будет изменяться и при уменьшении диапазона суммирования.

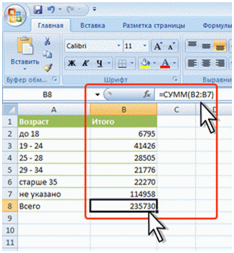
Рис.1.  Простое суммирование

Выборочная сумма

Иногда необходимо суммировать не весь диапазон, а только ячейки, отвечающие некоторым условиям (критериям). В этом случае используют функцию СУММЕСЛИ.

Синтаксис функции

СУММЕСЛИ(А;В;С),

где A – диапазон вычисляемых ячеек.

В – критерий в форме числа, выражения или текста, определяющего суммируемые ячейки;

С – фактические ячейки для суммирования.

В тех случаях, когда диапазон вычисляемых ячеек и диапазон фактических ячеек для суммирования совпадают, аргумент С можно не указывать.

Можно суммировать значения, отвечающие заданному условию. Например, в таблице на рис.2 суммированы только студенты по странам, при условии, что число студентов от страны превышает 200.

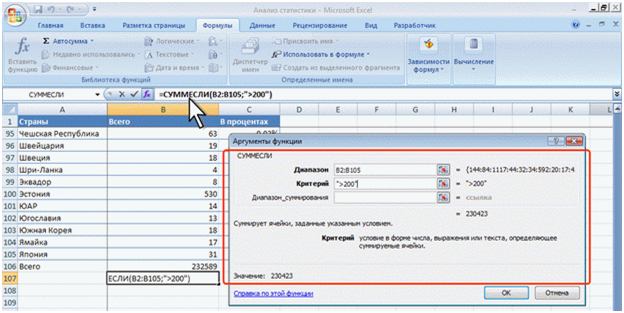
Рис.2.  Выборочное суммирование

Умножение

Для умножения используют функцию ПРОИЗВЕД.

Синтаксис функции

ПРОИЗВЕД(А),

где A – список от 1 до 30 элементов, которые требуется перемножить. Элемент может быть ячейкой, диапазоном ячеек, числом или формулой. Ссылки на пустые ячейки, текстовые или логические значения игнорируются.

Фактически данная функция заменяет непосредственное умножение с использованием оператора умножения (*). Так же как и при использовании функции СУММ, при использовании функции ПРОИЗВЕД добавление ячеек в диапазон перемножения автоматически изменяет запись диапазона в формуле. Например, если в таблицу вставить строку, то в формуле будет указан новый диапазон перемножения. Аналогично формула будет изменяться и при уменьшении диапазона.

Округление

Округление чисел особенно часто требуется при денежных расчетах. Например, цену товара в рублях, как правило, нельзя устанавливать с точностью более двух знаков после запятой. Если же в результате вычислений получается большее число десятичных разрядов, требуется округление. В противном случае накапливание тысячных и десятитысячных долей рубля приведет в итоге к ошибкам в вычислениях.

Для округления чисел можно использовать целую группу функций.

Наиболее часто используют функции ОКРУГЛ, ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ.

Синтаксис функции ОКРУГЛ

ОКРУГЛ(А;В),

где A – округляемое число;

В – число знаков после запятой (десятичных разрядов), до которого округляется число.

Возведение в степень

Для возведения в степень используют функцию СТЕПЕНЬ.

Синтаксис функции

СТЕПЕНЬ(А;В),

где A – число, возводимое в степень;

В – показатель степени, в которую возводится число.

Отрицательные числа можно возводить только в степень, значение которой является целым числом. В остальном ограничений на возведение в степень нет.

Для извлечения квадратного корня можно использовать функцию КОРЕНЬ.

Синтаксис функции

КОРЕНЬ(А),

где A – число, из которого извлекают квадратный корень.

Нельзя извлекать корень из отрицательных чисел.

Тригонометрические вычисления

В Microsoft Excel можно выполнять как прямые, так и обратные тригонометрические вычисления, то есть, зная значение угла, находить значения тригонометрических функций или, зная значение функции, находить значение угла.

Синтаксис всех прямых тригонометрических функций одинаков. Например, синтаксис функции SIN.

SIN(А),

где A – угол в радианах, для которого определяется синус.

Точно так же одинаков и синтаксис всех обратных тригонометрических функций. Например, синтаксис функции АSIN

АSIN(А),

где A – число, равное синусу определяемого угла.

Следует обратить внимание, что все тригонометрические вычисления производятся для углов, измеряемых в радианах. Для перевода в более привычные градусы следует использовать функции преобразования (ГРАДУСЫ, РАДИАНЫ) или самостоятельно переводить значения используя функцию ПИ().

Функция ПИ() вставляет значение числа (пи). Аргументов функция не имеет, но скобки после названия удалять нельзя.

Например, при необходимости рассчитать значение синуса угла, указанного в градусах, необходимо его умножить на ПИ()/180.

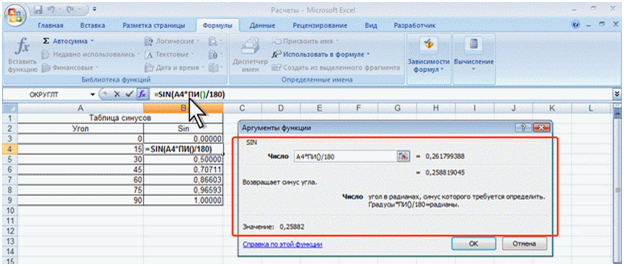
Рис.3  Вычисление тригонометрических функций для углов, указанных в градусах 

Преобразование чисел

Преобразование чисел может потребоваться при переводе углов из градусов в радианы и обратно, при определении абсолютной величины числа, при преобразовании арабских цифр в римские.

Для перевода значения угла, указанного в радианах, в градусы используют функцию ГРАДУСЫ.

Синтаксис функции

ГРАДУСЫ(А),

где А – угол в радианах, преобразуемый в градусы.

Для перевода значения угла, указанного в градусах, в радианы используют функцию РАДИАНЫ.

Синтаксис функции

РАДИАНЫ(А),

где А – угол в градусах, преобразуемый в радианы.

Для определения абсолютной величины числа используют функцию ABS. Абсолютная величина числа – это число без знака.

Синтаксис функции

ABS(А),

где А – число, для которого определяется абсолютное значение.

Генератор случайных чисел

В некоторых случаях на листе необходимо иметь число, которое автоматически и независимо от пользователя может принимать различные случайные значения.

Для создания такого числа используют функцию СЛЧИС(). Функция вставляет число, большее или равное 0 и меньшее 1. Новое случайное число вставляется при каждом вычислении в книге. Аргументов функция не имеет, но скобки после названия удалять нельзя.